

Both the Laplace transform and the inverse Laplace transform are used to analyze the dynamic control system. To analyze control systems, different functions will be carried out. It holds a significant role in control system engineering. Also, it is essential to have a complete understanding of the concept if you are working on mathematical concepts. This concept is used in a lot of domains. This is done so as to allow us to obtain multiple transforms of any function that does not have Fourier transforms. Laplace transform is considered a generalized Fourier series. It is considered the best way to convert an ordinary differential equation into algebraic equations and convolution into multiplication which aids in solving them faster and in a significantly easier approach. It changes one signal into another based on some fixed set of rules and equations. It is named after a great French mathematician, Pierre Simon De Laplace. Laplace transform, is an integral transform that converts a function of a real variable, usually time, to a function of a complex variable or complex frequency. You can join our courses to develop the advanced skills required to build your career and earn a certificate from renowned universities.
Great Learning offers Post Graduate Programs in various fields of sciences, management, and other additional skills. This course will give its subscribers good clarity on Laplace transformation, the first shifting theorem, and its various applications by solving multiple examples. This transform has various applications in different types of science and engineering since it is a tool used to solve differential equations. It is considered the best way to convert differential equations into algebraic equations and convolution into multiplication.
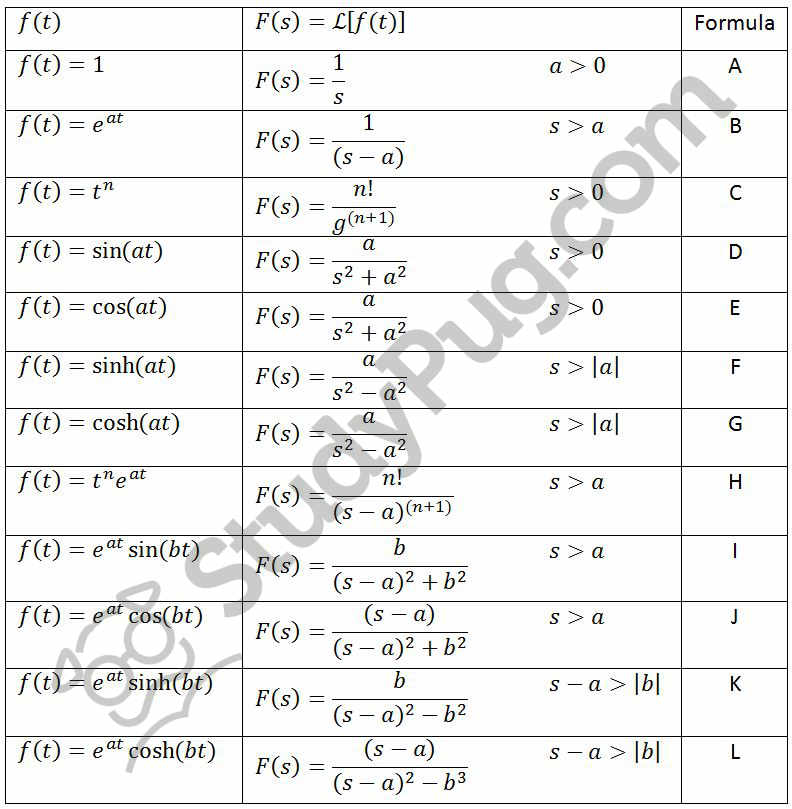
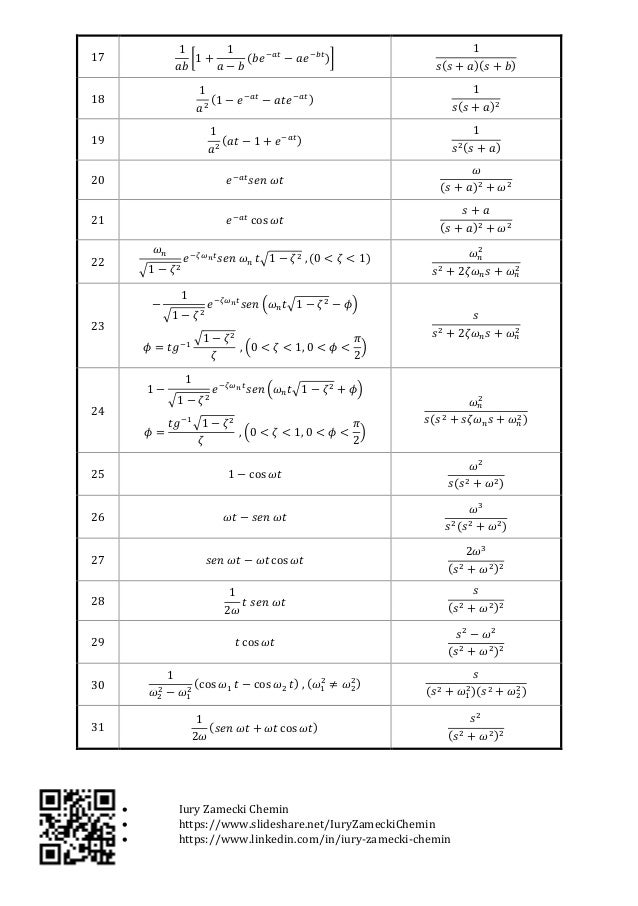
It changes one signal into another based on some fixed rules and equations. x(00) lim sX (s) 10.Laplace transform is an integral transform that converts a real variable function, usually time, to a function of a complex variable or complex frequency. Table 2.2.2 Properties of the Laplace transform X(s)=Jof()e dt aF(s)bG (s) x(t) af (t)bg (t) 1. $2(82 +b2) sin bt bt 2b3 sin bt- bt cos bt 27. constant, c u,(t-D), shifted unit step 4. Table 2.2.1 Table of Laplace transform pairs.
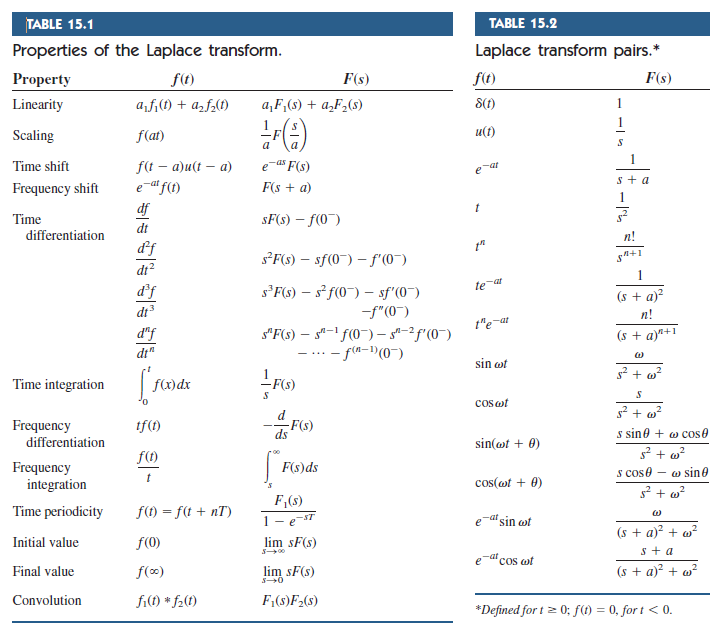
For part c, do not use # 11 in Table 2.2.1. For part b, do not use # 29 in Table 2.2.1. Specify which transform pair or property is used and write in the simplest form. Transcribed image text: Use the table of Laplace transforms and properties to obtain the Laplace transform of the following functions.


 0 kommentar(er)
0 kommentar(er)
